Robustness and Accuracy of Deep Learning Algorithms
Julius Berner, Philipp Grohs
Deep learning refers to the use of deep neural networks (DNNs) to represent complex systems such as speech, image perception, or physical models. These DNNs are inferred from data samples by a process called "training", that is implemented by minimizing an empirical loss function via stochastic gradient descent (SGD) algorithms, see Figure 1 for a schematic description. The goal of such an algorithm is to be as close as possible to the ground truth that produced the data samples. This closeness is measured via a suitable norm of a given Banach space Y. In classical ML the error is usually measured in terms of a generalization error defined as an expected value of a loss function. This quantity is highly dependent on the underlying data distribution and provides a measure of an average error. While such bounds may be sufficient for many applications, there are several problems where stronger notions of accuracy are needed - for example security critical applications that need to be safeguarded against a possible adversary, problems with a distribution shift where the data generating and data validation distributions differ, or applications in the computational sciences (for example in engineering applications) where a very high accuracy is mandatory. In all these problems it is imperative to guarantee a small error for every input data point, and not just on average - in other words, high accuracy with respect to Y = L∞. It has also been repeatedly observed that the training of neural networks (e.g., fitting a neural network to data samples) to high uniform accuracy presents a big challenge: conventional training algorithms (such as SGD and its variants) often find neural networks that perform well on average (meaning that they achieve a small generalization error), but there are typically some regions in the input space where the error is large; see Figure 3 for an illustrative example. This phenomenon is at the heart of several observed instabilities in the training of deep neural networks, including adversarial examples (see Figure 4 [5] or [1]), or so-called hallucinations emerging in generative modeling, e.g., tomographic reconstructions [2] or machine translation [3]. Such instabilities can be exploited by an adversary, for example to hack mobile phones by bypassing its (deep learning based) facial ID authentication [4]. These examples strongly indicate that many deep learning based systems are prone to being fooled, posing a crucial problem in any security-critical context.In the series of works [G1,G2,G3] we have developed mathematical techniques to prove that these phenomena are inherent to all deep-learning-based methods. More precisely, our results give sharp bounds on the sampling complexities of different neural network architectures, e.g., how many training samples are needed to guarantee a given accuracy with respect to the norm Y. A striking finding of our work is that, if the norm is given by the uniform L∞ norm, the resulting number of training samples becomes intractable. Figure 2 shows a simple neural network architecture consisting of less than 15000 free parameters. Our results show that any algorithm that provably trains such a neural network (with ReLU activation) to uniform accuracy 0.001 would need more training samples than there are atoms in the universe. Compare this to polynomial spaces which would only require 15000 samples to achieve zero error - the instability phenomenon is truly a property of neural networks. We anticipate that our results contribute to a better understanding of possible circumstances under which it is possible to design reliable deep learning algorithms and help explain well-known instability phenomena such as adversarial examples. To the best of our knowledge, we provide the first practically relevant bounds on the number of samples needed in order to completely prevent adversarial examples (on the whole domain). Such an understanding can be beneficial in assessing the potential and limitations of machine learning methods applied to security-critical scenarios and thus have a positive societal impact.
[1] Ian Goodfellow, Jonathon Shlens, and Christian Szegedy. Explaining and harnessing adversarial examples. In 3rd International Conference on Learning Representations, 2015.
[2] Sayantan Bhadra, Varun A Kelkar, Frank J Brooks, and Mark A Anastasio. On hallucinations in tomographic image reconstruction. IEEE transactions on medical imaging, 40(11):3249-3260,2021.
[3] Mathias Müller, Annette Rios Gonzales, and Rico Sennrich. Domain robustness in neural machine translation. In Proceedings of the 14th Conference of the Association for Machine Translation in the Americas, pages 151-164, 2020.
[4] Ron Shmelkin, Liar Wolf, and Tomer Friedlander. Generating master faces for dictionaryattacks with a network-assisted latent space evolution. In 16th IEEE International Conferenceon Automatic Face and Gesture Recognition, pages 01-08, 2021.
[5] Aleksander Mądry, Ludwig Schmidt (Jul 6, 2018). A Brief Introduction to Adverserial Examples. Retrieved from gradientscience.org/intro_adversarial/
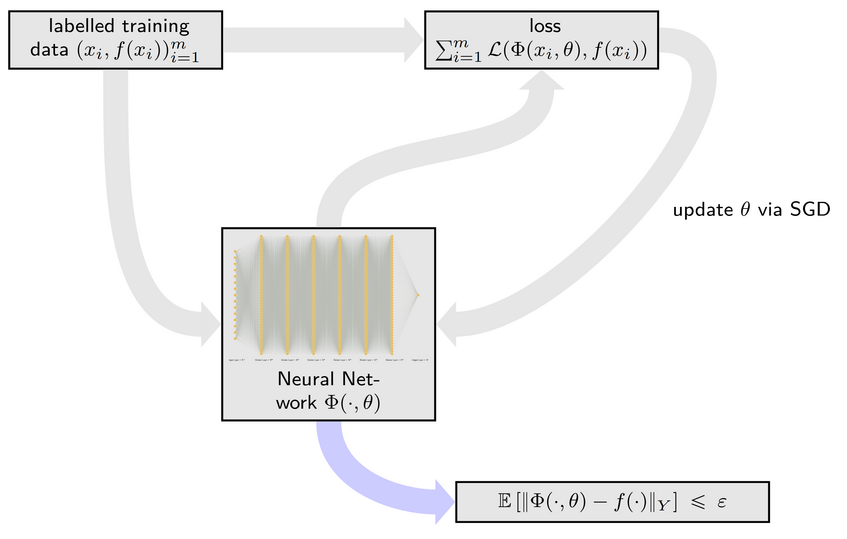
Figure 1: Schematic description of DNN training

Figure 2: NN architecture with less than 15000 free parameters. Training such a NN to three digits of accuracy with respect to the uniform norm would require more training samples than atoms in our universe
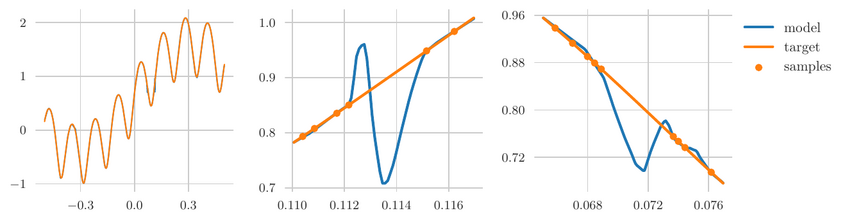
Figure 3: while NN training often provides reasonable accuracy on average, the uniform error is typically large

Figure 4: The inherent instability of NN training implies that NN based methods are inherently susceptible to adversarial attacks [5].
