DeepErwin - Accelerating computational chemistry using Deep Learning
Michael Scherbela, Leon Gerard, Rafael Reisenhofer, Philipp Marquetand, Philipp Grohs
Development of new materials – such as pharmaceuticals, semiconductors or catalysts – is a key driver of technological progress, but testing new materials in a lab is expensive and time consuming. To guide these experiments, we would ideally like to calculate properties for a large number of new molecules on a computer, with the aim of finding promising candidate molecules, which can then be synthesised and tested experimentally. This is in principle possible thanks to the Schrödinger equation, which describes the behaviour of the fundamental particles of a molecule, and thus its properties. Unfortunately, solving the Schrödinger equation exactly is only possible for extremely simple systems – for all interesting molecules, solutions can only be obtained numerically. Finding solutions is computationally extremely challenging, because established methods scale poorly with system size: Finding highly accurate solutions can take several days of computation even for relatively small molecules.
Recently unsupervised Deep-Learning based methods have been developed, which achieve unsurpassed accuracy while still providing promisingly low scaling of computational cost with the size of the molecule. These methods use a purposefully crafted Deep Neural Network to predict a solution to the Schrödinger equation, the so-called wavefunction. The network consists of multiple modules to capture the intricate physics of the wavefunction and roughly 200,000 free parameters / network weights. An optimization algorithm iteratively checks whether the predicted solution satisfies the Schrödinger equation and makes adjustments to the neural network weights until the solution satisfies the equation. Once the solution has been found, relevant properties of the molecule, such as its intrinsic energy can be easily computed. Importantly these methods work in an unsupervised fashion and do not require a training set of known reference solutions, but can instead generate high-accuracy solutions purely from the Schrödinger equation and a given geometry of a molecule.
While these methods offer high accuracy and good scaling with system size, they are currently still too expensive to calculate properties for many different molecules, or even just different geometries of a single molecule. The core problem is that these methods do not share information about solutions across different molecules and thus need to be expensively re-trained for every new geometry.
In our recent paper published in Nature Computational Science we demonstrate that we can substantially speed-up training when trying to find solutions for many different geometries of a molecule. We achieve this by sharing neural network weights across different networks being trained for different geometries. Thus any optimization of the network weights for one geometry, also benefits all other geometries. We find that up to 95% of network weights can be shared across geometries, and observe up to 16x speed-ups compared to traditional, independent optimizations.
Inspired by the success of transfer learning in other domains – the concept of using pre-trained parts of a neural network in a different setting, we also demonstrate the transferability of our neural network weights: Using weights pre-trained by our weight-sharing optimization substantially speeds up optimization for unseen geometries or even entirely different molecules.
To further speed up the search for promising molecules and their geometries, we have also implemented and demonstrated a method to compute quantum mechanical forces acting on molecules. This allows the efficient mapping of the so-called Potential Energy Surface (PES) of a molecule, depicting the energy of a molecule depending on its geometry. Understanding the PES of a molecule is important to many properties of a molecule, such as its shape, resistance to distortions, infrared spectrum or even thermal stability.
There are still many open questions to be explored: How can this approach be further improved to enable calculations of larger molecules? How could the method be adapted to also work for solid materials beyond isolated molecules? Could we train the model on a large variety of different molecules and share the weights as a universally pre-trained model, similarly to successes in pre-trained models for natural language processing or image recognition? We tackle these and related questions within our research group, hoping to further advance available techniques for materials research.
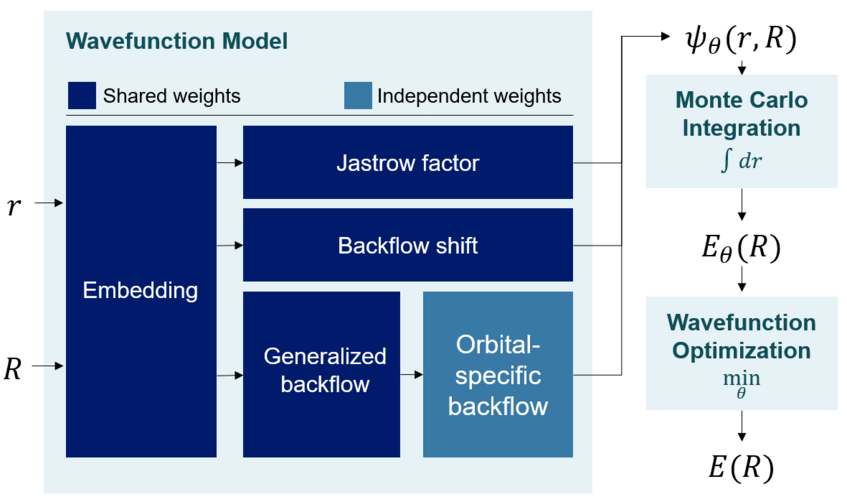
Overview of the Deep Neural Network: It takes as input the coordinates of electrons and nuclei – the fundamental particles forming a molecule – and predicts the wavefunction . Using a technique called Monte Carlo Integration the algorithm checks how well the prediction satisfies the Schrödinger equation and makes adjustments until a satisfactory wavefunction has been found. When repeating this for different molecules or geometries we can re-use and share a majority of the network weights in our wavefunction model.
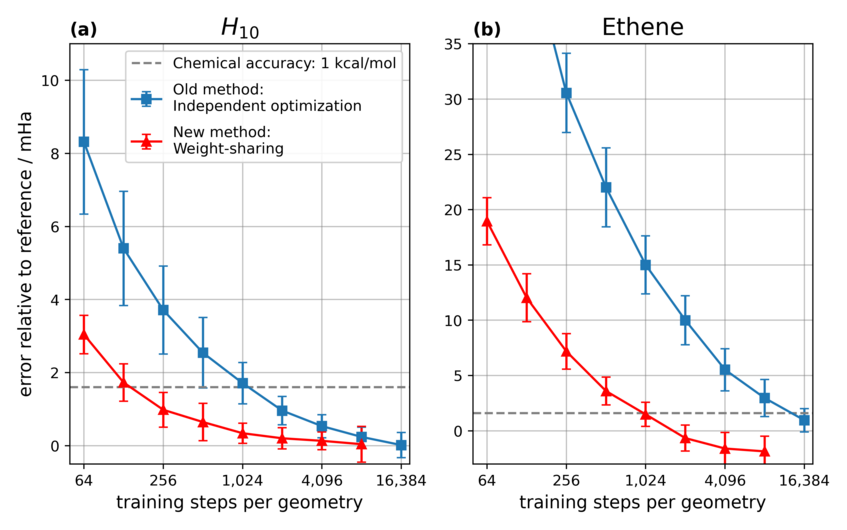
Results of weight-sharing vs. independent optimization: Deviation of the calculated energies for 2 different molecules (H10 and ethene) relative to a classical high-accuracy method (lower is better) for different number of training steps. With more training steps accuracy improves for both methods, but the new weight-sharing approach reaches good levels of accuracy much faster than independent optimization (note the log-scale).
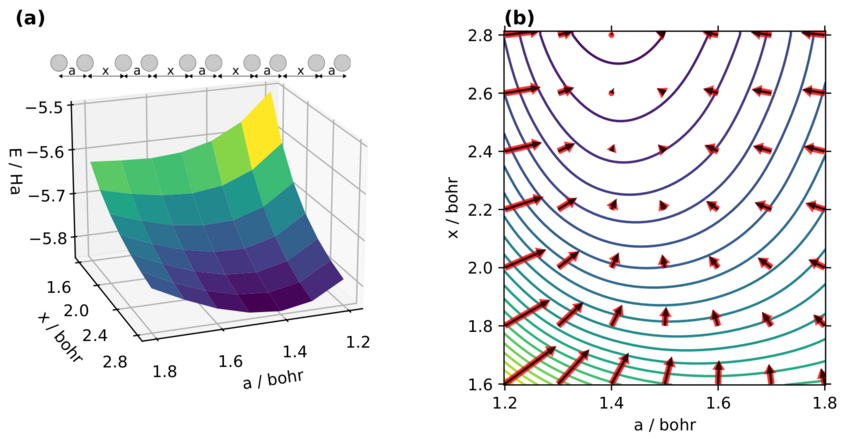
Example of a potential energy surface (PES): a) Energy of a chain of Hydrogen atoms, depending on the distances between them b) Same PES, additionally showing the forces acting on the nuclei (arrows) pushing the molecule into a low-energy geometry
Press releases
Schnelleres Deep Learning für rechnergestützte Chemie (Medienportal Universität Wien)
Schnelleres Deep Learning für rechnergestützte Chemie (LISA Vienna)
Wiener Forscher nehmen Moleküleigenschaften mittels KI unter die Lupe (APA Science)
Vorhersage von Moleküleigenschaften durch Lösen der Schrödinger Gleichung (Analytik News)
