Phase Retrieval
Lukas Liehr, Martin Rathmair, Philipp Grohs
In various branches of physics and the engineering sciences, one aims at extracting information about a certain object of interest (for instance, the structure of a crystal, the composition of a material, audio signals, properties of quantum mechanical systems, ...) from so-called intensity-only measurements, i.e. measurements without phase information. Such measurements appear due to experimental restrictions and physical limitations of the devices used to perform the measurement. The recovery of the phase from intensity-only measurements forms the class of phase retrieval problems. These problems have confounded mathematicians, physicists, and engineers for many decades. The perhaps most prominent example of a phase retrieval problem arises in the field of diffraction imaging. Here the task is to recover an object from a diffraction pattern which appears as the result of measuring the intensities of a diffracted wave which is sent to the object. One can show that the diffraction pattern is the absolute value of the Fourier transform or the short-time Fourier transform (STFT) of the object.
The arising phase retrieval problem is commonly known as the Fourier resp. STFT phase retrieval problem. This is a non-linear inverse problem. The aim of our research group is to obtain a precise understanding of this inverse problem by investigating uniqueness, stability, discretization and the design of stable algorithms. We tackle this problem from several directions using mathematical techniques from a variety of fields such as complex analysis, functional analysis, spectral geometry, sampling theory and numerical analysis. Currently, our main focus lies in the analysis of the STFT phase retrieval problem.
Uniqueness, discretization, sampling. Classical results in time-frequency analysis state that (under some mild conditions) a signal is uniquely determined by samples of its STFT. Do these results generalize to the setting where only samples of the magnitude of the STFT are available? In our recent paper [1] we reveal a fundamental difference to the setting where phase information is available: uniqueness can be never achieved from magnitude samples on a lattice, no matter how the window function is given and no matter how dense the lattice is chosen. Our results complement earlier work [2] where we proved uniqueness results from lattice samples under support conditions and restrictions to shift-invariant structures. Based on these results the investigation continues in several directions: can uniqueness be achieved from non-uniform sampling sets? Is the restriction to real-valued functions enough to achieve uniqueness from lattice samples? Which window functions and what signal classes guarantee unique recovery from spectrogram samples?
Stability. When dealing with real-world data, the study of stability of the phase retrieval problem is essential, due to the occurrence of measurement errors, imprecision of machine arithmetic or imperfect modeling. Hence a stability analysis of the phase retrieval problem is essential. In [3] and [4] we were able to show that for Gaussian windows, stability is equivalent to the connectedness of the measurements. More precisely, we obtained stability estimates in terms of a constant arising in the field of spectral clustering, namely the Cheeger constant. In [5] we elaborated these results in several directions, for instance, by studying discrete stability estimates.
Design of stable algorithms. Recent years have witnessed a surge in the systematic understanding of computational algorithms for phase retrieval. The design of stable algorithms forms a cornerstone in the field of phaseless signal reconstruction. For instance in [6], we derived a provably stable and convergent approximation technique for functions in Gaussian shift-invariant spaces from spectrograms samples.
References.
[1] On foundational discretization barriers in STFT phase retrieval. Liehr, Lukas; Grohs, Philipp.
[2] Injectivity of Gabor phase retrieval from lattice measurements. Grohs, Philipp; Liehr, Lukas.
[3] Stable Gabor Phase Retrieval and Spectral Clustering. Grohs, Philipp; Rathmair, Martin.
[4] Stable Gabor phase retrieval for multivariate functions. Grohs, Philipp; Rathmair, Martin.
[5] L2-stability analysis for Gabor phase retrieval. Grohs, Philipp; Rathmair, Martin.
[6] Stable Gabor phase retrieval in Gaussian shift-invariant spaces via biorthogonality. Liehr, Lukas; Grohs, Philipp.
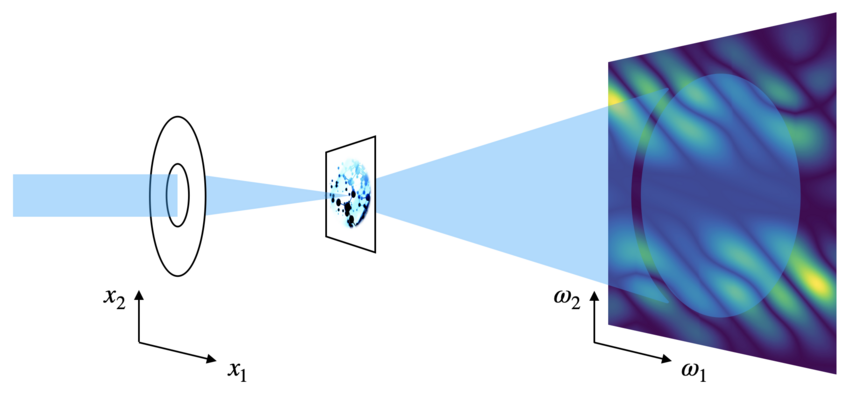
Principle of ptychography.

Difference of two spectrograms.
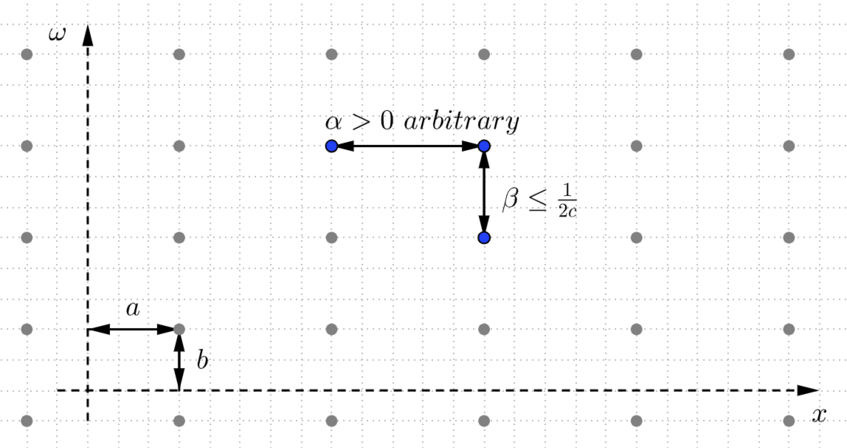
Lattice in the time-frequency plane. Spectrogram samples given on this lattice determine compactly supported functions.

Cheeger cuts.
