Machine Learning based numerical methods for high dimensional PDEs
Julius Berner, Lukas Herrmann, Philipp Grohs
PDEs are among the most important and widely used modeling principles. Examples include the Schrödinger equation in quantum chemistry, Vlasov-Poisson equations arising in cosmological simulations and astrophysical models, and Kolmogorov equations such as Fokker–Planck equations and the so-called chemical master equation arising in the life sciences or in computational finance. In optimal control Hamilton-Jacobi-Bellman like equations are of paramount importance. These equations are all high dimensional and often non-linear, generally with non-smooth solutions. Considering and modeling parametric dependencies increases the problem's dimensionality even further. This makes the development of efficient numerical algorithms extremely challenging.
A key challenge lies in the fact that most classical numerical function representations suffer from the curse of dimension, meaning that exponentially many parameters in the input dimension to accurately capture a given PDE solution. In order to circumvent these issues, we explore the use of neural networks as a numerical ansatz.
For several such models (particularly for parabolic PDEs such as Black-Scholes PDEs or Hamilton-Jacobi-Bellman PDEs) we could for the first time prove that neural networks are capable of breaking the curse of dimension [1,3]. This means that solutions of these equations can be approximated to a given accuracy by neural networks with their number of parameters only scaling polynomially in the dimension and in the reciprocal of the accuracy. We further showed, by reformulating a given parabolic PDE as a learning problem, see Figure 1, that these approximate solutions can in principle be “learned” from polynomially many data samples [2]. Based on these results we have constructed competitive numerical solvers for parametric Black Scholes equations [4]. Our numerical results (see also github.com/mdsunivie/deep_kolmogorov) strongly indicate that the algorithmic complexity of our algorithms does not suffer from the curse of dimension, either, see Figure 2.
In ongoing and future work we aim to extend these results to nonlinear PDEs with possibly non smooth solutions. For this we also explore alternative numerical representations that are only partially based on neural networks.
[1] P Grohs, F Hornung, A Jentzen, P Von Wurstemberger. A proof that artificial neural networks overcome the curse of dimensionality in the numerical approximation of Black-Scholes partial differential equations.
Memoirs of the American Mathematical Society
[2] J Berner, P Grohs, A Jentzen. Analysis of the generalization error: Empirical risk minimization over deep artificial neural networks overcomes the curse of dimensionality in the numerical approximation of Black-Scholes PDEs.SIAM Journal on Mathematics of Data Science 2 (3), 631-657
[3] P Grohs, L Herrmann. Deep neural network approximation for high-dimensional parabolic Hamilton-Jacobi-Bellman equation.
arXiv preprint arXiv:2103.05744
[4] J Berner, M Dablander, P Grohs. Numerically solving parametric families of high-dimensional Kolmogorov partial differential equations via deep learning. Advances in Neural Information Processing Systems 33, 16615-16627
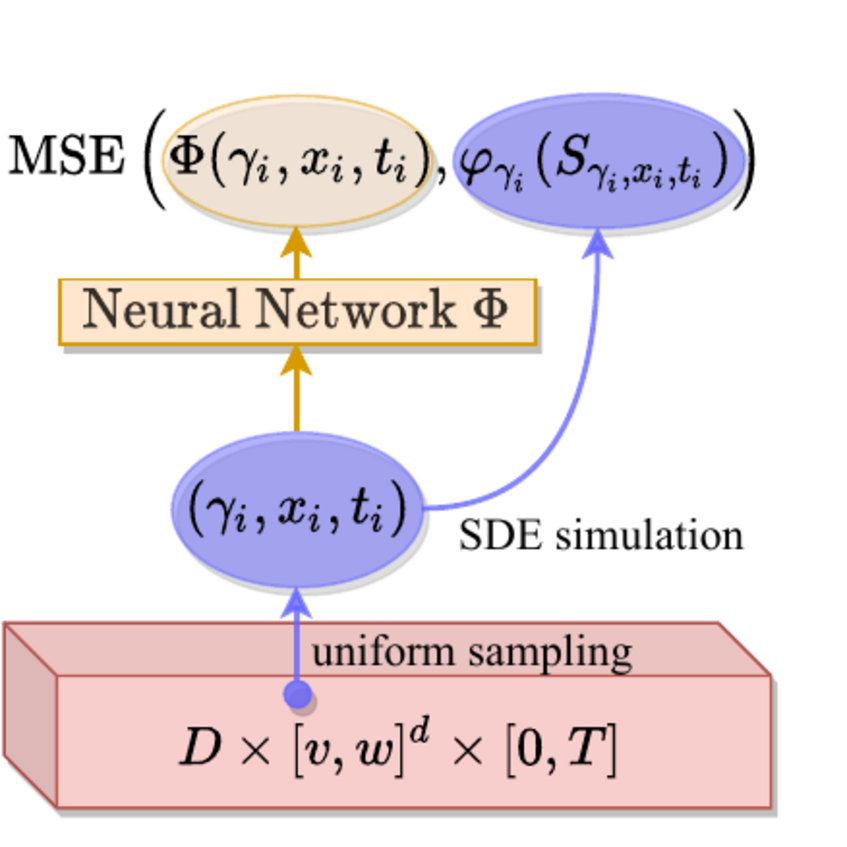
Figure 1: Parabolic PDEs can be reformulated as a standard learning problem using the Feynman-Kac formula
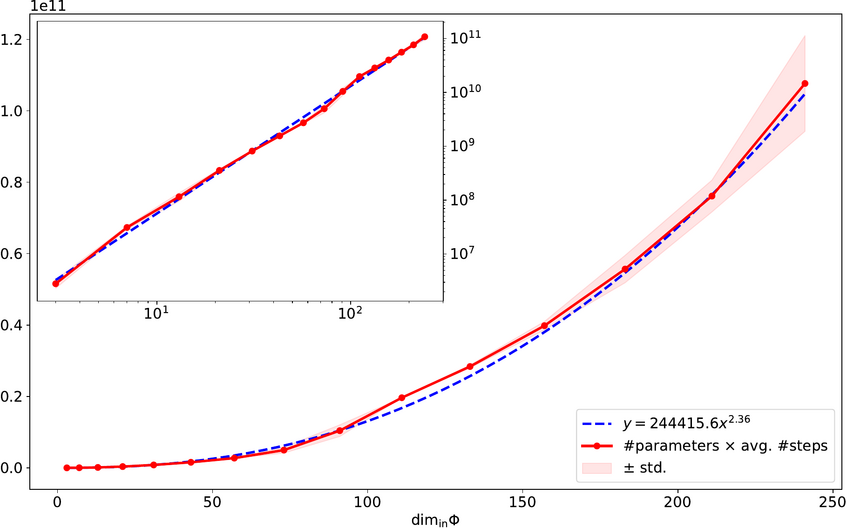
Figure 2: computational cost vs input dimension for the numerical algorithm introduced in [4]. The plot strongly suggests the absence of the curse of dimension
