Welcome to our website
The research group Mathematical Data Science, headed by Univ.-Prof. Dr. Philipp Grohs, represents the area of data science, particularly in relation to different aspects of applied mathematics.
Its research is motivated by interdisciplinary applications and ranges from theory over algorithm development to the solution of real-world problems.
We have made, and continue to make progress in several different areas, including
the development of mathematical theory for deep learning algorithms with the goal of extending the scope of applications of deep learning towards problems that require some degree of “understanding” of the data’s inherent characteristics and the structure of the domain they come from,
the development and rigorous analysis of machine learning algorithms for the numerical solution of high dimensional problems in science and engineering that cannot be efficiently solved by existing methods, and
the mathematical analysis of phase retrieval problems that constitute a major challenge in various applications such as coherent diffraction imaging.
Our research software is hosted on github.com/mdsunivie.
Research Highlights
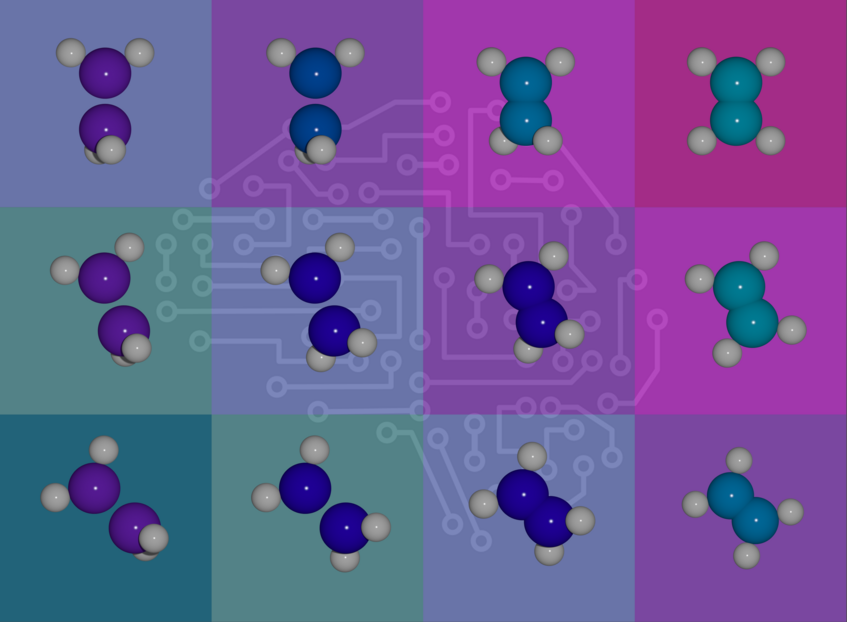
DeepErwin: Solving the Schrödinger equation
Development of new molecules, such as pharmaceuticals, is a key driver of technological progress, but testing them in a lab is slow and expensive. To accelerate this process, methods have been developed to predict properties of molecules on a computer by solving the Schrödinger equation. However, due to the high dimensionality of the problem established methods are often either too slow or not accurate enough. Our method dubbed DeepErwin tackles the Schrödinger Equation by combining Deep Neural Networks and Monte Carlo methods. In recent work we show how we can reach superior accuracy compared to established methods, and how we can get solutions for many different molecules at once.
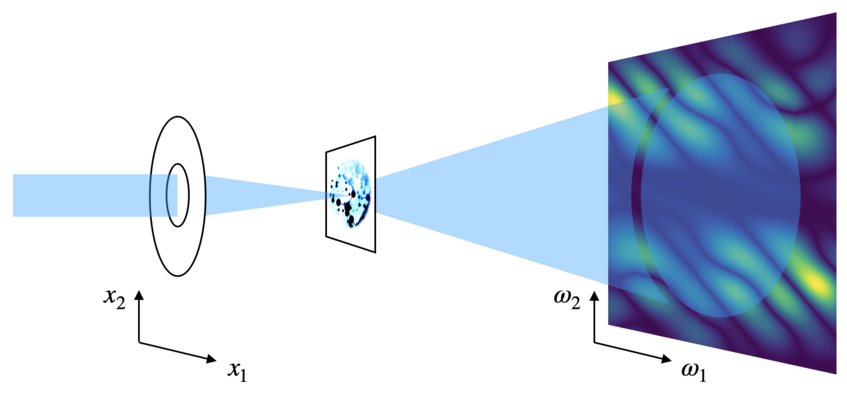
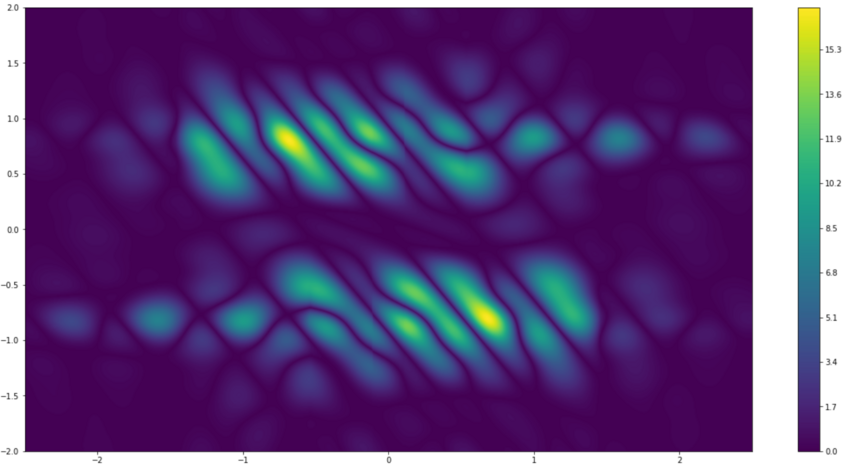
Phase Retrieval
In various branches of physics and the engineering sciences, one aims at extracting information about an object of interest from intensity-only measurements. The recovery of the phase from such measurements forms the class of phase retrieval problems. These problems have confounded mathematicians, physicists, and engineers for many decades and constitute a highly active research area. The goal of our research group is to obtain a precise mathematical understanding of the phase retrieval problem by investigating uniqueness, stability, discretization and the design of stable algorithms. Currently, our main focus lies in the analysis of the STFT phase retrieval problem.
Robustness and Accuracy of Deep Learning Algorithms
For several applications --- for example in a security-critical context or for problems in the computational sciences --- one would like to have guarantees for high accuracy of a deep learning algorithm on every input value, that is, with respect to the uniform norm. We prove that, under very general assumptions, the minimal number of training samples for this task scales exponentially both in the depth and the input dimension of the network architecture, rendering the training of ReLU neural networks to high uniform accuracy intractable. In a security-critical context this points to the fact that deep learning based systems are prone to being fooled by a possible adversary. In ongoing work we aim to use our improved understanding of the weaknesses of standard deep learning algorithms to design improved models.
Machine Learning based numerical methods for high dimensional PDEs
PDEs are among the most important and widely used modeling principles. Examples include the Schrödinger equation in quantum chemistry, Vlasov-Poisson equations arising in cosmological simulations and astrophysical models, and Kolmogorov equations such as Fokker–Planck equations and the so-called chemical master equation arising in the life sciences or in computational finance. In optimal control Hamilton-Jacobi-Bellman like equations are of paramount importance. These equations are all high dimensional and often non-linear, generally with non-smooth solutions. Considering and modeling parametric dependencies increases the problem's dimensionality even further. This makes the development of efficient numerical algorithms extremely challenging. In our work we design neural network based representations for solutions of these PDEs and corresponding algorithms that can provably break the curse of dimension.
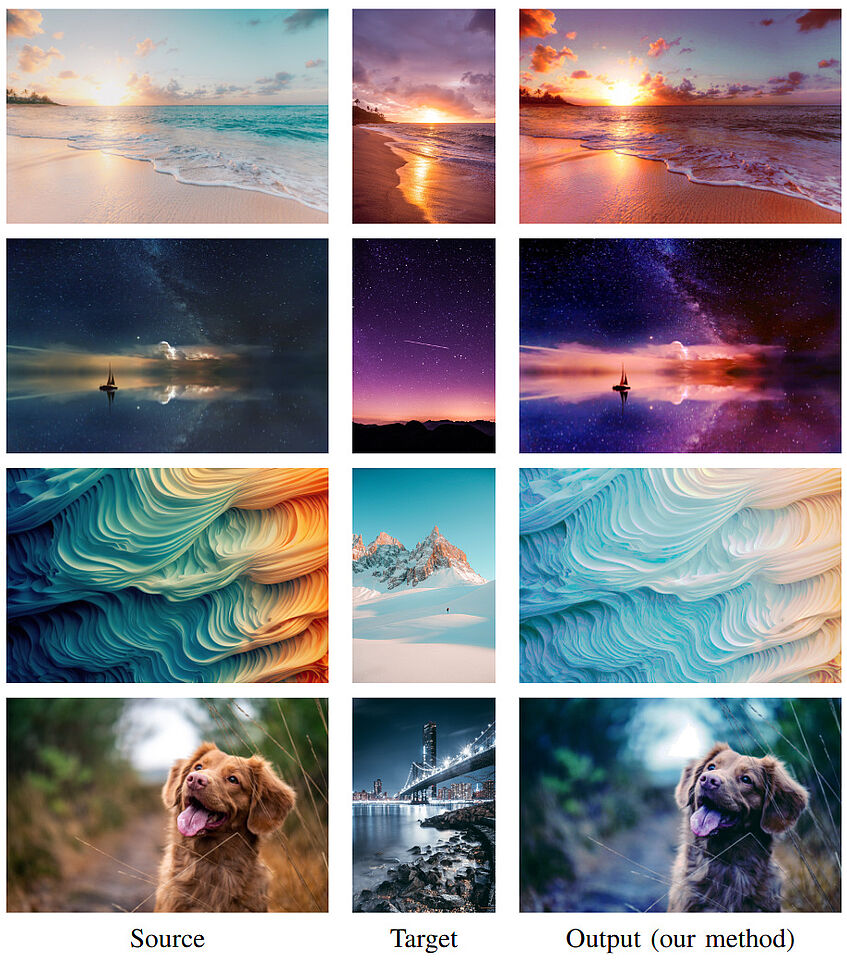
FakET: Simulating Cryo-Electron Tomograms with Neural Style Transfer
In cryo-electron microscopy, accurate particle localization and classification are imperative. Recent deep learning solutions, though successful, require extensive training data sets. The protracted generation time of physics-based models, often employed to produce these data sets, limits their broad applicability. In this work we demonstrate that Neural Style Transfer, a technique traditionally employed for manipulating natural images, can be successfully adapted to simulate cryo-electron micrographs or tilt-series. This application provides the means to generate high-quality, fully-labeled data for training deep neural networks, enhancing their efficacy on downstream tasks within computational microscopy.

Redistributor: Transforming Empirical Data Distributions
We present an algorithm and package, Redistributor, which forces a collection of scalar samples to follow a desired distribution. When given independent and identically distributed samples of some random variable S and the continuous cumulative distribution function of some desired target T, it provably produces a consistent estimator of the transformation R which satisfies R(S)=T in distribution. As the distribution of S or T may be unknown, we also include algorithms for efficiently estimating these distributions from samples. This allows for various interesting use cases in image processing, where Redistributor serves as a remarkably simple and easy-to-use tool that is capable of producing visually appealing result. For color correction it outperforms other model-based methods and excels in achieving photorealistic style transfer, surpassing deep learning methods in content preservation. The package is implemented in Python and is optimized to efficiently handle large datasets, making it also suitable as a preprocessing step in machine learning.